Funkcja wykładnicza – funkcja postaci:
- f(x) = ax, gdzie a > 0.
Własności :
- Pochodna funkcji wykładniczej to:
Czyli w szczególności dla
 mamy
mamy- Funkcja wykładnicza o podstawie a > 1 jest (przy argumencie dążącym do
 ) asymptotycznie większa niż funkcja wielomianowa, mniejsza zaś niż silnia.
) asymptotycznie większa niż funkcja wielomianowa, mniejsza zaś niż silnia.
Szczególnym przypadkiem funkcji wykładniczej jest funkcja eksponencjalna, czyli funkcja wykładnicza o podstawie równej e (czyli podstawie logarytmu naturalnego). Inne oznaczenie takiej funkcji to: exp(x) (nazywane skrótowo eksponentą).
Cechą funkcji
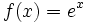 jest to, że jej pochodna jest równa jej samej. Eksponens jako funkcję analityczną na mocy twierdzenia Taylora można rozwinąć w szereg potęgowy:
jest to, że jej pochodna jest równa jej samej. Eksponens jako funkcję analityczną na mocy twierdzenia Taylora można rozwinąć w szereg potęgowy:  .
.Wykres funkcji
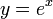 :
:
Funkcja Wykładnicza : http://www.youtube.com/watch?v=kP8uaXfKuTE



 funkcja wykładnicza o podstawie
funkcja wykładnicza o podstawie  jest
jest 
 to funkcja
to funkcja 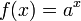 jest stała.
jest stała.

Brak komentarzy:
Prześlij komentarz